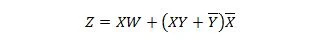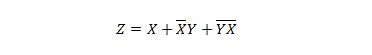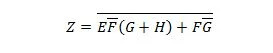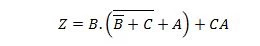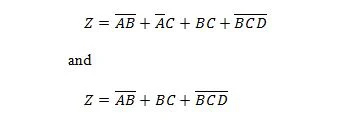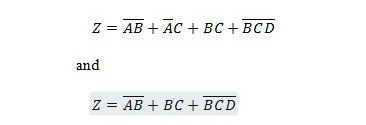2. poglavje: Boolova algebra in z njo povezane računalniške komponente
2.1 Osnovni logični operatorji
Predpostavi, da sem jaz (avtor) visok in ti (bralec) si visok. Če bi vas nekdo vprašal, ali sva oba visoka, bi rekli 'Da' (res). Če vpraša, ali sva oba nizka, bi rekel 'Ne' (false). Če ste vi nizki in sem jaz visok, in vas vpraša, ali ste vi ali jaz visoki, bi bil vaš odgovor 'Da' (res). Če vpraša, ali sva oba visoka, ne bi imel odgovora. Lahko bi rekli, da se zadnje vprašanje ne bi smelo postaviti ali da vprašanje nima odgovora. No, želim, da ti (bralec) veš, da je treba danes v določenih okoliščinah postaviti vprašanje.
V biologiji je človek visok ali nizek. »Okoljski« pogoji so tisti, zaradi katerih je oseba srednje visoka. En znanstvenik, George Boole, je opredelil vrsto odgovorov ali pravil za tovrstna vprašanja. Ta pravila se bomo naučili v tem delu spletnega kariernega tečaja (poglavje). Ta pravila se danes uporabljajo v računalništvu, programiranju, elektroniki in telekomunikacijah. Pravzaprav brez teh pravil ne bi imeli računalnika, kot je danes običajno; ne bi imeli tudi programiranja, kot je danes običajno.
Pravilno ali napačno
Preprosta izjava v človeškem jeziku je sama po sebi resnična ali napačna. Če rečem 'visok sem', je to ali res ali napačno. Če rečem 'visok si', je to res ali ne. Če sem jaz visok, ti pa nizek in se postavi vprašanje, ali sva oba visoka, je v Boolovi logiki treba dati odgovor res ali napačno. Katerega od teh dveh je treba dati? Boole pravzaprav ni odgovoril na to vprašanje. Preprosto je pripravil niz pravil, ki se jih moramo držati. Dobra novica je, da ko upoštevate ta pravila v njihovem pravem kontekstu, nimate dvoumnosti. Zahvaljujoč tem pravilom imamo danes računalnike in programiranje. Pravila so vam dana. Pravil res ni mogoče razložiti; jih samo sprejmeš. Pravila so pod tremi naslovi: IN, ALI in NE.
IN
Vprašanje se lahko postavi, če sva oba ti IN jaz visoka. Moja višina in tvoja višina sta nato združeni z nizom pravil IN. To so pravila IN, ki jih morate upoštevati:
false IN false = false
false IN true = false
resnično IN napačno = napačno
res IN res = res
Zdaj naj bo visok resničen in nizek napačen. To pomeni, da če sem jaz nizek IN si ti nizek, sva ti in jaz nizka. Če sem jaz nizek IN si ti visok, sva ti in jaz nizka; to je logični odgovor, ki ga morate sprejeti. Če sem jaz visok IN si ti nizek, sva oba nizka. Če sem jaz visok IN si ti visok, sva ti in jaz visoka. Vse to so IN logična pravila, ki jih morate (bralec) samo sprejeti.
ALI
Vprašanje se lahko postavi, če si ti ALI jaz visok. Moja višina in tvoja višina sta nato združeni z nizom pravil ALI. To so pravila ALI, ki jih morate upoštevati:
false ALI false = false
false ALI true = res
res ALI napačno = res
res ALI res = res
Še enkrat, naj bo visok resničen in nizek napačen. To pomeni, da če sem jaz nizek ALI si ti nizek, si nizek ti ALI jaz. Če sem jaz nizek ALI si ti visok, sem visok ti ali jaz. Če sem jaz visok ALI si ti nizek, si ti ALI jaz visok. Če sem jaz visok ALI si ti visok, si visok ti ali jaz. Vse to so logična pravila, ki jih morate sprejeti.
NE
V logični logiki obstajata le dve stanji (možna odgovora). Se pravi, če NISI visok, si nizek. Če NISI kratek, si visok; nič drugega. To so pravila, ki jih NE morate upoštevati:
NI napačno = res
NI resnično = napačno
Predpostavimo, da imate vrvico (ali vzmet), ki jo lahko podaljšate (potegnete). Medtem ko je vrvica v svojem naravnem stanju, če rečem 'NI kratka', bi jo podaljšali; to je interpretacija. Medtem ko je niz podaljšan, če rečem 'NI dolg', bi mu dovolili, da se skrči; to je interpretacija.
Zapomniti si morate vsa dana pravila v njihovih različnih kategorijah.
Več kot dva operanda
V računalniškem jeziku se IN, ALI in NE vsak imenujejo operator. Za operator NOT potrebujete samo en operand (vrednost za operator), da dobite odgovor. Za operatorja AND ali OR imate lahko več kot dva operanda. Prejšnji primeri prikazujejo dva operanda za IN in ALI. Za IN lahko imate tri operande, kot sledi:
napačno IN napačno IN napačno = napačno
napačno IN napačno IN resnično = napačno
To sta dve vrstici; vsak ima dva operatorja IN. Če so operandi trije, je dejansko devet vrstic. Z operatorjem AND je le zadnja vrstica (deveta vrstica) enaka true; vse prejšnje vrstice so napačne. Upoštevajte, da je pri dveh operandih za IN samo zadnja vrstica še vedno resnična; vse prejšnje tri vrstice so napačne. Če so operandi štirje, je 16 vrstic in samo zadnja vrstica velja za operator IN.
Vzorec za IN in vzorec za ALI sta različna. S tremi operandi za dva operatorja ALI je tudi devet vrstic in samo prva vrstica je tokrat napačna. Od druge do devete vrstice je res. Upoštevajte, da je pri dveh operandih za ALI samo prva vrstica še vedno resnična; vse preostale tri vrstice so napačne. Če so operandi štirje za ALI, je tudi 16 vrstic.
Operator NOT obravnava samo en operand. NOT false je res in NOT true je false.
2.2 Resnična tabela dveh operandov in njune elektronske komponente
V matematiki obstaja tema, imenovana algebra. Majhen del tega smo videli v prejšnjem poglavju. Obstaja neke vrste algebra, imenovana Boolovska algebra. V Boolovi algebri je resnica identificirana z osnovno dvomestno številko, ki je 1, napačna pa z osnovno dvomestno številko, ki je 0.
Komponente notranje računalniške enote so elektronske komponente. Sistemska enota računalniškega sistema ima digitalne elektronske komponente. Operacijo IN izvaja majhna elektronska komponenta, imenovana vrata IN. Operacijo ALI izvaja majhna elektronska komponenta, imenovana vrata ALI. Operacijo NOT izvaja majhna elektronska komponenta, imenovana vrata NOT. Preveč teh vrat je lahko v čipu integriranega vezja (IC).
IN miza resnice in njena vrata
Naslednja tabela podaja tabelo resnic IN in njen simbol vrat IN (majhno vezje):
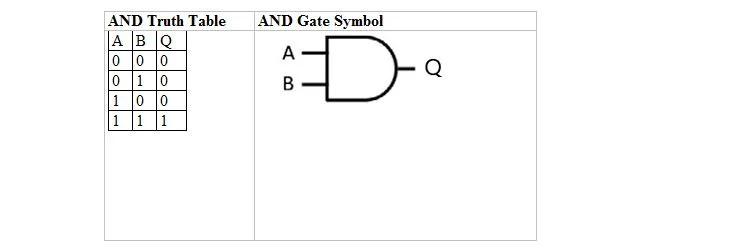
Za tabelo resnic IN in njena vrata sta A in B dve vhodni spremenljivki. Q je izhodna spremenljivka. A je 1 ali 0. B je 1 ali 0. Q je 1 ali 0. Tabela resnic IN z 1 in 0 je enaka kot prejšnja postavitev resnic (tabela) resnic/neresnic IN. Enačba IN je:
A . B = Q
kjer pika (.) pomeni IN (logično). Piko lahko izpustite, da bo AB = Q, kar pomeni isto (IN).
Opomba: Bita za A in B v štirih vrsticah, kot pari, so prve štiri številke v osnovi dve, ki se začnejo z 0 (ali 00), tj. 00, 01, 10, 11.
Naslednja tabela prikazuje tabelo resnic ALI in njen simbol vrat ALI (majhno vezje):
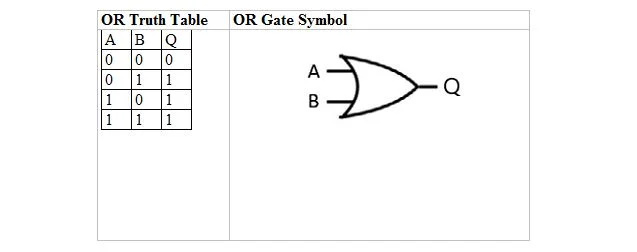
Za tabelo resnic ALI in njena vrata sta A in B dve vhodni spremenljivki. Q je izhodna spremenljivka. Tabela resnic ALI z 1 in 0 je enaka prejšnji postavitvi (tabeli) resničnosti ALI resnic.
Enačba ALI je:
A + B = Q
Kjer + tukaj pomeni logični ALI in ne seštevanja. Enačba se bere kot 'A ali B je enako Q'.
Naslednja tabela podaja tabelo resnic NOT in njen simbol NOT vrat (majhno vezje):
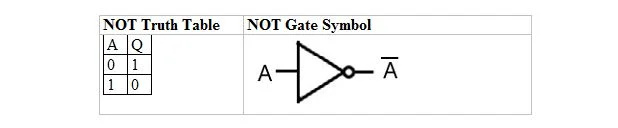
Tabela resnic NOT ali vrata NOT imajo samo en vhod in en izhod. Ko je vhod 0, je izhod 1. Ko je vhod 1, je izhod 0. Vrata NOT naredijo nekakšno inverzijo. Izhodna spremenljivka je enaka vhodni spremenljivki, vendar s črto (prečrtano). Tabela resnic NE z 1 in 0 je enaka kot prejšnja postavitev (tabela) resničnosti resnice ALI resnice.
Enačba NE je:
A = Q
Kjer je Q = A in prečka nad A tukaj pomeni komplement. Komplement 0 je 1 in komplement 1 je 0. Vrata NE so znana tudi kot INVERTIRAJoča vrata.
To so temeljne (ali korenske) tabele resnic in njihova vrata (majhna vezja) v digitalni elektroniki (z Boolovo algebro). Druge tri tabele resnic, ki so podane na naslednji ilustraciji, in njihova vrata so namenjeni priročnosti in temeljijo na prejšnjih treh tabelah resnic.
Obstajajo tabela resnic in vrata, ki izhajajo iz tabele in vrat resnic IN. Imenujejo se tabela resnic NAND (za NE IN) in ustrezna vrata NAND. Tabela resnic NAND in njena vrata NAND so:
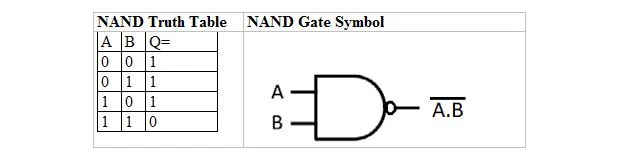
Če želite pridobiti tabelo resnic NAND, pojdite na izhod tabele resnic IN in zamenjajte vsako števko z njenim komplementom. Komplement 0 je 1 in komplement 1 je 0. Vrata NAND so kot vrata IN, vendar imajo majhen krog pred izhodno vrstico. Enačba NAND je:
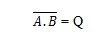
Kjer pomeni komplement rezultata 'A' IN 'B'. Palica (nadčrta) je v vratih predstavljena z majhnim krogom. Upoštevajte, da lahko piko med A in B izpustite.
Obstaja še ena tabela resnic in vrata, ki izhajajo iz tabele resnic in vrat ALI. Imenujejo se tabela resnic NOR (za NE ALI) in ustrezna vrata NOR. Tabela resnic NOR in njena vrata NOR so:
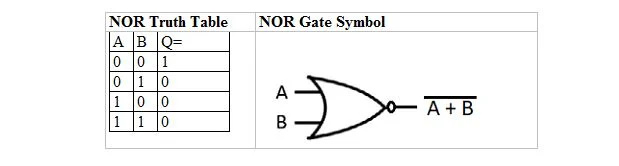
Če želite pridobiti tabelo resnic NOR, pojdite na izhod tabele resnic OR in zamenjajte vsako števko z njenim komplementom. Komplement 0 je 1 in komplement 1 je 0. Vrata NOR so podobna vratim ALI, vendar imajo majhen krog pred izhodno vrstico. Enačba NOR je:
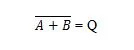
Kje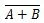 
pomeni dopolnilo rezultata 'A' ALI 'B'. Vrstica (nadčrta) je v vratih predstavljena z majhnim krogom.
Izključni ALI (XOR)
Tabela resnic za vrata ALI je:
V običajni angleščini ni jasno, ali mora zadnja vrstica 1 ALI 1 dati 1 ali 0. Torej, v Boolovi algebri obstajata dve vrsti tabel resnic ALI in dve ustrezni vrati. Pri običajnem ALI daje zadnja vrstica 1 ALI 1 1. Druga vrsta ALI je izključni ALI (XOR), kjer so prve tri vrstice enake kot prve tri vrstice običajnega ALI (vključno z izhodom). Vendar pa za četrto in zadnjo vrstico 1 ALI 1 da 0.
Naslednja tabela prikazuje tabelo resnic XOR in njen simbol vrat XOR (majhno vezje):
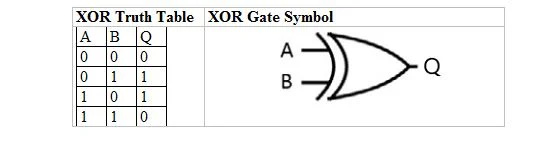
Za tabelo resnic XOR in njena vrata sta »A« in »B« dve vhodni spremenljivki. 'Q' je izhodna spremenljivka.
Enačba XOR je:
A ⊕ B = Q
Kjer ⊕ tukaj pomeni logični XOR.
Običajni ALI pomeni eno ali oboje. Izključni ALI pomeni strogo bodisi in ne oboje.
2.3 Logični postulati
Postulati so predpostavke, na podlagi katerih se izpeljejo določeni zaključki. Obstaja deset Boolovih postulatov, ki izhajajo iz enačb IN, ALI in NE (tabel resnic). Te enačbe imenujemo tudi funkcije. Osnovne funkcije so kopirane na naslednji način:
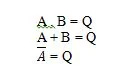
To so temeljne funkcije (enačbe) v Boolovi algebri. Naslednje druge tri (funkcije) enačbe niso temeljne funkcije:
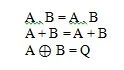
Čeprav je zadnja funkcija tukaj nenavadna, se ne šteje za temeljno funkcijo.
Logični postulati so naslednji:
Iz funkcije IN
1) 0 . 0 = 0
dvajset. 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Iz funkcije ALI
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Iz funkcije NOT
9) 0 = 1
10) 1 = 0
Opomba: Ti postulati so le vrstice v tabelah resnic IN, ALI in NE, ki so izražene na neodvisen način. Bralec naj si zapomni podane postulate.
2.4 Logične lastnosti
Lastnost je podobna značilnost nečesa. Logične lastnosti so enačbe, ki izhajajo iz logičnih postulatov. V tem razdelku so lastnosti preprosto podane brez izpeljav in nato uporabljene pozneje. Obstaja petindvajset lastnosti, ki so razvrščene pod deset naslovov, kot sledi:
Lastnosti funkcije IN
Lastnost 1:
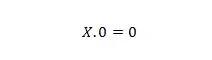
Kjer je X lahko 1 ali 0. To pomeni, da je ne glede na to, kaj je X, rezultat vedno 0.
Opomba: Spremenljivka ne sme biti nujno A ali B ali C ali D. Spremenljivka je lahko W ali X ali Y ali Z ali katera koli druga črka.
Lastnost 2:
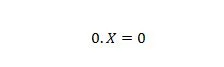
Kjer je X lahko 1 ali 0. Upoštevajte, da je razlika med lastnostjo 1 in lastnostjo 2 v tem, da sta na levi strani enakega znaka obeh enačb položaji X in 0 zamenjani.
Lastnost 3:
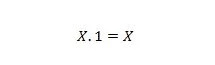
Če je X 0, potem je 0. 1 = 0. Če je X 1, potem je 1. 1 = 1.
Lastnost 4:
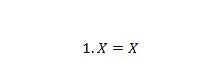
Če je X 0, potem je 1. 0 = 0. Če je X 1, potem je 1. 1 = 1. Upoštevajte, da je razlika med lastnostjo 3 in lastnostjo 4 v tem, da so na levi strani obeh enačb položaji X in 1 se zamenjata.
Lastnosti funkcije OR
Lastnost 5:
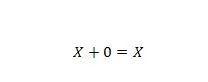
Kjer je X lahko 1 ali 0. To pomeni, da če je X 0, je rezultat 0. Če je X 1, je rezultat 1.
Lastnost 6:
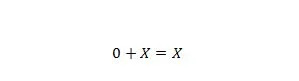
Kjer je X lahko 1 ali 0. Upoštevajte, da je razlika med lastnostjo 5 in lastnostjo 6 ta, da sta na levi strani obeh enačb položaji X in 0 zamenjani.
Lastnost 7:
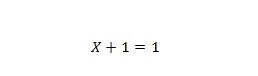
Če je X 0, potem je 0 + 1 = 1. Če je X 1, potem je 1 + 1 = 1.
Lastnost 8:
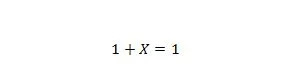
Če je X 0, potem je 1 + 0 = 1. Če je X 1, potem je 1 + 1 = 1. Upoštevajte, da je razlika med lastnostjo 7 in lastnostjo 8 v tem, da so na levi strani obeh enačb položaji X in 1 se zamenjata.
Lastnosti v zvezi s kombinacijo spremenljivke s samo seboj ali njenim komplementom
Lastnost 9: 
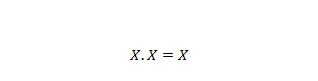
To je: če je X 0, potem je 0. 0 = 0. Če je X 1, potem je 1 . 1 = 1.
Lastnost 10:
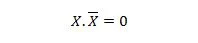
To pomeni: če je X 0, potem je 0. 1 = 0. Če je X 1, potem je 1. 0 = 0.
Za zaporedne spremenljivke ta lastnost postane:
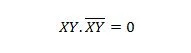
Lastnost 11:
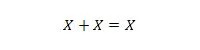
To pomeni: če je X 0, potem je 0 + 0 = 0. Če je X 1, potem je 1 + 1 = 1 (iz običajnega ALI).
Lastnost 12:
To pomeni: če je X 0, potem je 0 + 1 = 1. Če je X = 1, potem je 1 + 0 = 1.
To pomeni: če je X 0, potem je 0 + 1 = 1. Če je X = 1, potem je 1 + 0 = 1.
Dvojno dopolnjevanje
Lastnost 13:
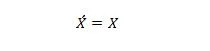
Ko je X na levi strani 0, X na desni strani postane 0. Ko je X na desni strani 1, X na levi strani postane 1. Z drugimi besedami, dvojna dopolnila vrnejo prvotno vrednost.
Komutativno pravo
Lastnost 14:
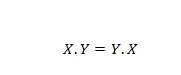
To pomeni, da zamenjava prvega in drugega operanda za operator IN na levi strani znaka enačaja ni pomembna; odgovor je po opravljeni menjavi na levi strani še vedno enak. To enačbo lahko zapišemo z izpuščenimi pikami kot: XY = YX.
Lastnost 15:
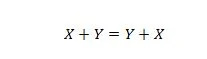
Razlaga tukaj je enaka kot v prejšnjem IN, vendar je za operator OR.
Distributivni zakon
Lastnost 16:
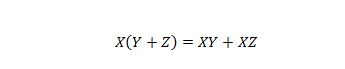
Tukaj so tri spremenljivke: X, Y in Z. Vsaka spremenljivka je lahko 1 ali 0. Oklepaji na levi strani simbola enakovrednosti pomenijo, da najprej ocenite, kaj je v njih. Nato je IN rezultat z X. Desna stran pravi, da sta X IN Y skupaj ALI X IN Z skupaj enaka levi strani. Upoštevajte, da je operator pike za IN izpuščen vseskozi; in združene spremenljivke še vedno pomenijo IN.
Lastnost 17:
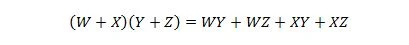
Ta lastnost je razširitev lastnosti 16 z dodano spremenljivko W.
Asociativno pravo
Lastnost 18:
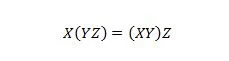
Oklepaji pomenijo, da najprej ocenite, kaj je v oklepajih. Torej, za izraz na levi strani, če sta Y z Z najprej AND in X je AND z rezultatom, potem je ta končni rezultat na levi strani enak končnemu rezultatu na desni -hand-side, kjer se X z Y najprej izvede AND, preden se rezultat izvede z Z. Upoštevajte, da so bile pike v enačbi izpuščene.
Lastnost 19:
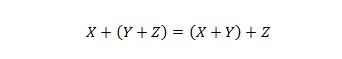
Ta lastnost je razložena na podoben način kot lastnost 18, vendar je namesto operatorja IN uporabljen operator ALI. Operator OR + ni nikoli izpuščen iz logičnega izraza zaradi enostavnosti. Po drugi strani pa lahko operator IN izpustite in obe spremenljivki združite.
Absorpcija
Lastnost 20:
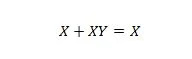
S to enačbo, ne glede na to, kaj je Y, bo desna stran vedno X (absorbirana).
Lastnost 21:
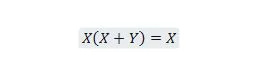
Tudi pri tej enačbi bo desna stran vedno X (absorbirana), ne glede na to, kaj je Y. Ta lastnost 21 je enaka lastnosti 20, ki je:
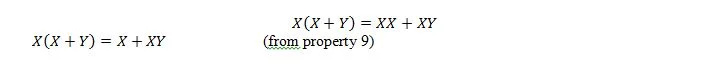
Tu uporabljamo distribucijski zakon in dejstvo, da je X.X = X lastnosti 9.
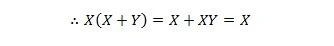
Identiteta
Lastnost 22:
To pomeni, da za izraz X + Y komplement X pred Y ne spremeni izraza.
Lastnost 23:
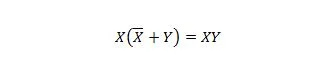
To pomeni, da za izraz XY dopolnitev X ALI z Y v oklepaju, ki se izvede najprej, ne spremeni izraza XY.
DeMorganov zakon
Lastnost 24:
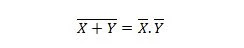
To pomeni, da imajo vrata NOR (NOT OR) enak rezultat kot NOTing dveh vhodov pred IN.
Lastnost 25:
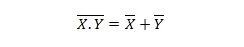
To pomeni, da imajo vrata NAND (NE IN) enak rezultat, kot če NE označite dva vhoda pred ALI.
Predložene ilustracije so 25 lastnosti. Lahko jih dokažemo s substitucijo vseh različnih možnih vrednosti 1 in 0 v vsakem izrazu na levi strani, da vidimo, ali je dobljen izraz (ali rezultat) na desni strani. Dokazi so puščeni kot vaja za bralca.
2.5 Poenostavitev sestavljenih izrazov
Naslednji dve funkciji sta enaki:
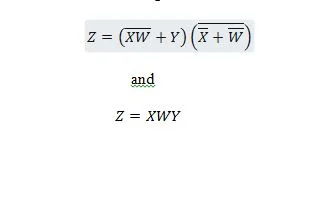
Z je izhod, X, W in Y pa vhodi. Prvi potrebuje vrata NAND, vrata ALI, vrata IN, dve vrati NE, vrata ALI in vrata NI. Drugi potrebuje samo dve vrati IN. Prva je enačba s sestavljenim izrazom na desni strani, ki je bil poenostavljen (zmanjšan) na en izraz na desni strani za drugo enačbo.
Poenostavitev ali redukcija vodi do manjšega števila vrat, da se izvede enaka funkcija kot vezje. Tako manjše vezje je lahko del integriranega vezja (IC) ali samostojno vezje na površini matične plošče računalnika.
Ko funkcija (enačba) prispe v proces načrtovanja, je treba izvesti poenostavitev, da se zmanjša število vrat in na koncu dobimo cenejše vezje. Za poenostavitev je potrebna uporaba ene ali več od prejšnjih petindvajsetih logičnih lastnosti.
Primer 2.51:
Zmanjšaj enačbo:
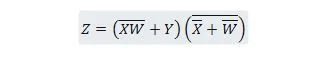
Opomba: Dva oklepaja drug zraven drugega pomenita, da sta oklepaja dodana IN (pika med njima opcijsko ni zapisana).
rešitev:
Pri rešitvah je utemeljitev (razlog) za vsak korak navedena na desni strani koraka v oklepaju. Bralec naj prebere vsak korak in njegovo utemeljitev. Bralec naj se pri branju korakov zmanjšanja funkcije obrne tudi na prejšnje lastnosti.
Primer 2.52:
Poenostavite:
2.6 Najmanjša vsota produktov
Naslednji dve funkciji sta enaki:
Oba izraza na desni strani obeh enačb naj bi bila v obliki vsote produktov (SP). Ekspresni izraz je v obliki vsote produkta, če nima oklepajev. Očitno je, da prva funkcija (enačba) potrebuje več vrat kot druga funkcija.
Prvi desni izraz je še vedno mogoče zmanjšati, da dobimo drugo funkcijo. Drugega izraza na desni strani ni mogoče še naprej poenostavljati in ga še vedno izraziti kot vsoto zmnožkov (»seštevanje« členov). Drugega izraza na desni strani pravzaprav ni več mogoče poenostaviti. Torej naj bi bil v obliki minimalne vsote produktov (MSP).
Primer 2.61:
Prinesite naslednjo funkcijo najprej v obrazec Vsota zmnožkov in nato v obrazec Najmanjša vsota zmnožkov.
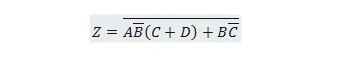
rešitev:
Pri reševanju takšnih problemov je treba uporabiti eno ali več od prejšnjih petindvajsetih lastnosti, kot je prikazano v tej rešitvi:
2.6 Najmanjša vsota produktov
Naslednji dve funkciji sta enaki:
Oba izraza na desni strani obeh enačb naj bi bila v obliki vsote produktov (SP). Ekspresni izraz je v obliki vsote produkta, če nima oklepajev. Očitno je, da prva funkcija (enačba) potrebuje več vrat kot druga funkcija.
Prvi desni izraz je še vedno mogoče zmanjšati, da dobimo drugo funkcijo. Drugega izraza na desni strani ni mogoče še naprej poenostavljati in ga še vedno izraziti kot vsoto zmnožkov ('seštevek' izrazov). Drugega izraza na desni strani pravzaprav ni več mogoče poenostaviti. Torej naj bi bil v obliki minimalne vsote produktov (MSP).
Primer 2.61:
Prinesite naslednjo funkcijo najprej v obrazec Vsota zmnožkov in nato v obrazec Najmanjša vsota zmnožkov.
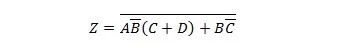
rešitev:
Pri reševanju takšnih problemov je treba uporabiti eno ali več od prejšnjih petindvajsetih lastnosti, kot je prikazano v tej rešitvi:
Ta zadnji izraz je v obrazcu za vsoto produktov (SP), vendar ne v obrazcu za najmanjšo vsoto produktov (MSP). Na prvi del vprašanja je odgovorjen. Rešitev za drugi del je naslednja:
Ta zadnja poenostavljena funkcija (enačba) je v obliki MSP in potrebuje manjše število vrat za izvedbo kot ustrezna oblika SP. Ne pozabite: SP pomeni vsoto produktov, medtem ko MSP pomeni najmanjšo vsoto produktov.
Primer 2.62:
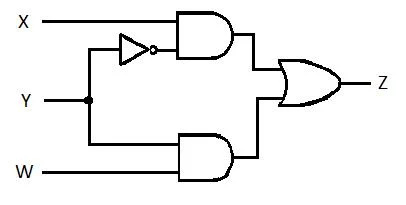
Naslednje vezje ima vhode X, Y in W, Z pa je izhod. Izdelajte funkcijo vsote zmnožkov (SP) (navidezno najmanjšo funkcijo vsote zmnožkov) za Z. Nato izdelajte pravo bolj zmanjšano (minimizirano) vsoto zmnožkov (MSP). Nato implementirajte vezje MSP (narišite mrežo vrat MSP).
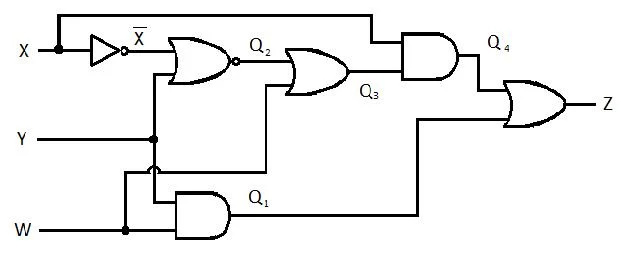
Slika 2.61 Zaporno vezje
rešitev:
Preden se začne postopek poenostavljanja, je treba izraz za Z pridobiti v smislu X, Y in W. Glejte ta primer ilustracije iz diagrama:
To je izraz Z v smislu X, Y in W. Po tem lahko pride do poenostavitve na navidezni MSP. Navidezni MSP je SP.
Ta zadnja enačba (funkcija) je v obliki SP. Ni resnična minimalna vsota produktov (še ni MSP). Torej se mora zmanjševanje (minimiziranje) nadaljevati.
Ta zadnja enačba (funkcija) je prava minimalna vsota produktov (MSP). Najmanjša vsota produktov (resnično minimiziranje) je:
Slika 2.62 Zaporno vezje MSP
Komentiraj
Iz analize v tem razdelku je razvidno, da ni jasno, ali je vsota zmnožkov najmanjša vsota zmnožkov ali ne. SP ni preveč uporaben. Prav MSP je zelo uporaben. Obstaja zagotovljen način za pridobitev MSP; to je uporaba Karnaughovega zemljevida. Zemljevid Karnaugh presega obseg tega spletnega kariernega tečaja.
2.7 Težave
Bralcu svetujemo, da reši vse težave v poglavju, preden se premakne na naslednje poglavje.
- Izdelajte tabele resnic IN, ALI in NE z ustreznimi vrati.
- Zapišite deset Boolovih postulatov v njihove različne kategorije in poimenujte kategorije.
- Brez razlage zapišite šestindvajset lastnosti Boolove algebre v njihove različne kategorije in poimenujte kategorije.
- Zmanjšajte enačbo z uporabo logičnih lastnosti in navajanjem uporabljenih kategorij.
- Zmanjšajte enačbo z uporabo logičnih lastnosti in navajanjem uporabljenih kategorij.
- Z uporabo logičnih lastnosti in navajanjem uporabljenih kategorij zmanjšajte naslednjo enačbo – najprej na vsoto zmnožkov in nato na najmanjšo vsoto zmnožkov:
- Z uporabo logičnih lastnosti in navajanjem uporabljenih kategorij zmanjšajte naslednjo enačbo – najprej na vsoto zmnožkov in nato na najmanjšo vsoto zmnožkov:
